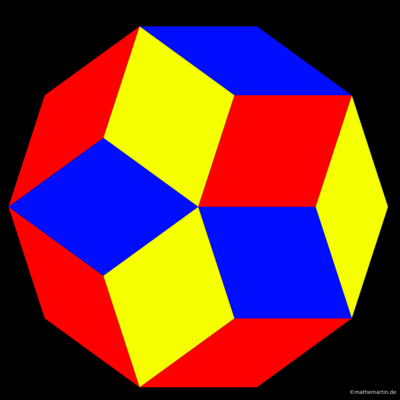
Sternpolygone
Rautensterne
Ich habe aus konzentrisch angeordneten Rauten mit Hilfe eines in Python geschriebenen Programmes Mandalas erstellt. Diese zeichnen sich dadurch aus, dass der 360°-Winkel im Zentrum in gleich große Winkel aufgeteilt wird. Ich habe diese Mandalas Rautensterne genannt. Je nachdem, in wie viele Teile n der Winkel aufgeteilt wird, bezeichne ich den Rautenstern als n-Rautenstern. Die Rauten haben alle dieselbe Seitenlänge. Die n vom Zentrum ausgehenden Winkel werden zu Rauten ergänzt. Die Winkel zwischen den neuen Seiten definiert den Winkel der nächsten Schicht an Rauten. Es werden so lange neue Schichten hinzugefügt, bis der neue Winkel, der ensteht, 180° überschreitet oder erreicht. Die enstandenen Sterne habe ich auf unterschiedliche Weise in einem Bildbearbeitungsprogramm coloriert.
Das Programm, das ich geschrieben habe, zeichnet in Abhängigkeit von n die Seiten der Rauten. Für n=3 ergibt sich ein dreigeteiltes Sechseck. Für große n bilden sich immer deutlicher Spiralarme heraus. Hier ein paar uncolorierte Beispielausgaben:
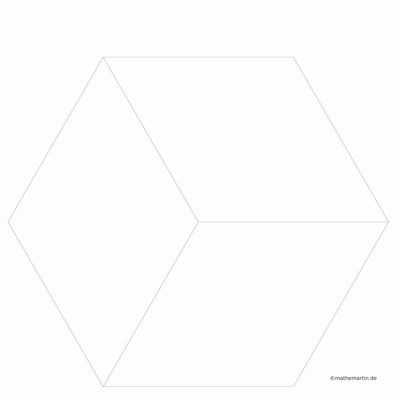
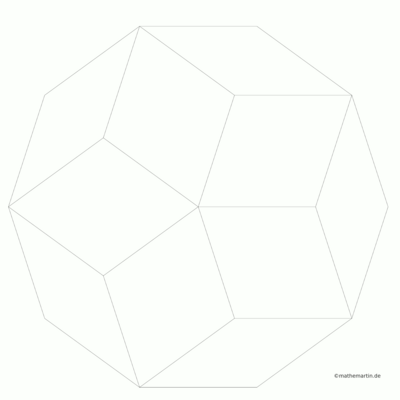
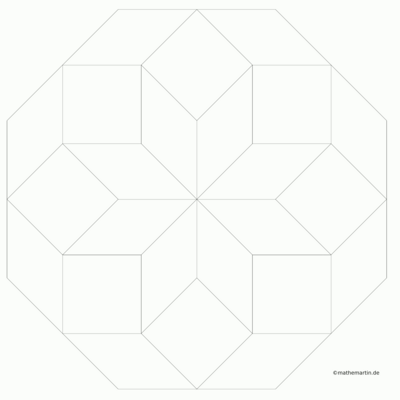
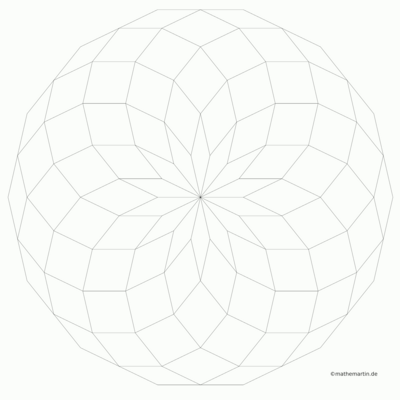

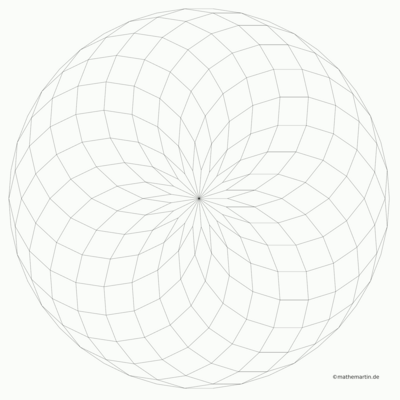
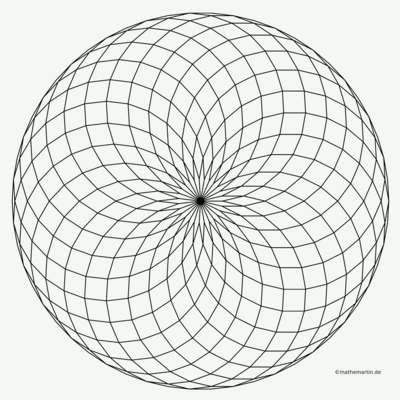

from numpy import *
from matplotlib.pyplot import *
class rautenstern:
def __init__(self,n):
self.__ecken=int(n)
self.__schalen=int(ceil(n/2))
self.plotter()
def phi(self,schale):
return 2*schale/self.__ecken*pi
def alpha(self,ecke,schale):
ecke=mod(ecke,self.__ecken)
if mod(schale,2)==1:
return ecke*2*pi/self.ecken
else:
return ecke*2*pi/self.ecken+pi/self.ecken
def r(self,schale):
rlist=[]
for j in range(1,schale):
if mod(j,2)!=mod(schale,2):
rlist.append(2*cos(self.phi(j)/2))
if mod(schale,2)==0:
return sum(rlist)
else:
return sum(rlist)+1
def x(self,r,alpha):
return r*cos(alpha)
def y(self,r,alpha):
return r*sin(alpha)
def plotter(self):
for schale in range(1,self.__schalen+1):
for ecke in range(self.ecken):
if schale==1:
alpha2=self.alpha(ecke,1)
r2=1
x2=self.x(r2,alpha2)
y2=self.y(r2,alpha2)
plot([0,x2],[0,y2],'k',linewidth='0.1')
elif mod(schale,2)==1:
alpha1=self.alpha(ecke-1,schale-1)
alpha2=self.alpha(ecke,schale)
alpha3=self.alpha(ecke,schale-1)
r1=self.r(schale-1)
r2=self.r(schale)
r3=self.r(schale-1)
else:
alpha1=self.alpha(ecke,schale-1)
alpha2=self.alpha(ecke,schale)
alpha3=self.alpha(ecke+1,schale-1)
r1=self.r(schale-1)
r2=self.r(schale)
r3=self.r(schale-1)
if schale>1:
x1=self.x(r1,alpha1)
y1=self.y(r1,alpha1)
x2=self.x(r2,alpha2)
y2=self.y(r2,alpha2)
x3=self.x(r3,alpha3)
y3=self.y(r3,alpha3)
plot([x1,x2,x3],[y1,y2,y3],'k',linewidth='0.1')
axis('square')
def export(self):
name='raute'+str(self.ecken)+'.png'
savefig(name,dpi=1000,bbox_inches='tight')
clf()
@property
def ecken(self):
return self.__ecken
@property
def schalen(self):
return self.__schalen
Sternpolygone
Ein regelmäßiges Sternpolygon ist durch die Eckpunkte eines regelmäßigen Polygons definiert, die durch gerade Strecken derart miteinander verbunden sind, dass keine 2 benachbarten Punkte und kein Punkt mit sich selbst verbunden ist. Dabei muss der letzte Eckpunkt wieder mit dem Anfangspunkt verbunden werden. Das einfachste Beispiel für so ein Sternpolygon ist das Pentagramm. Besonders schön sieht es aus, wenn beim Verbinden der Eckpunkte immer die gleiche Zahl an Ecken "übersprungen" wird. Man kann solche Sterne mit dem Schläfi-Symbol {m/n} kategorisieren. Dabei ist m die Anzahl der Zacken des Sterns und n die Anzahl der Ecken, die zwei verbundene Ecken voneinander "entfernt" sind. Ich habe mit Hilfe von Computerprogrammen mehrere ineinander verschachtelte Sternpolygone gezeichnet und coloriert.







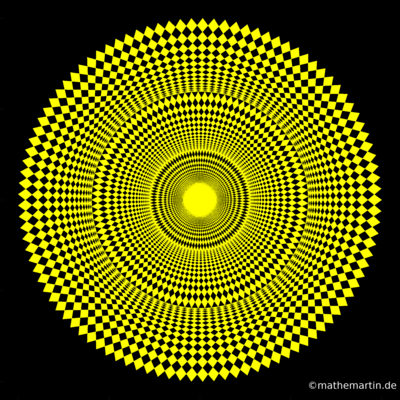

Variationen von Sternpolygonen


Bei einem Sternpolygon liegen die Zacken auf einer Kreislinie. Bei den folgenden Variationen habe ich diese gedachte Kreislinie durch eine Kurve ersetzt, deren Radialkoordinate sinusförmig von der Winkelkoordinate abhängt.




Mandalas